Rosana Zenil-Ferguson

Assistant Professor. University of Kentucky

State dependent diversification models

Instructors

  1. Carrie Tribble PhD Candidate. University of California Berkeley.

  2. Daniel Caetano. Postdoctoral researcher. Universidade de São Paulo, Brazil.

  3. Rosana Zenil-Ferguson Assistant Professor. University of Hawai’i Mānoa.

Background

The goal of this workshop is to get you familiarized with state dependent diversification models. In the literature they are called state dependent speciation and extinction, because the models link the value of the states to the rates of speciation and extinction. This idea will be clearer as we work through the workshop excercises.

Introduction to Bayesian Statistics and inference

For background infromation about some basic Bayesian statistics and MCMC algorithm to obtain posterior distribution samples plese reafer to the the slides below. This slides are from a short intro workshop I taught in Botany 2018 (Rochester, MN).

  1. Bayesian stats slides here
  2. Markov chain Monte Carlo (MCMC) slides here

We really suggest you watch the great introductory lecture from Dr. Paul Lewis available in this video.

Introduction to Continuous Time Markov Chains (CTMC)

Continuous time Markov chains are our power tools when we are trying to model any discrete trait evolution in a phylogeny. CTMCs are stochastic processes, that is a random variable that we follow throughout time that is measuring the outcome of interest.

The slides below are from the Botany workshop in 2018

  1. Continuous Time Markov Chains slides here

but more detailed background information can be found in this long lecture Rosana taught in the Midwest Phylogenetic Methods Workshop in 2019

  1. CTMC lecture.
  2. RevBayes code mk2.Rev

Basic installation of RevBayes and software for the workshop

In order to make it as efficient as possible the workshop please follow these steps.

  1. Make sure you have access to a command line. For mac users the terminal works fine, for windows users see this option If you are not too familiar with the command line check this very short tutorial

  2. Install RevBayes try to do it in a folder where you could find easily from the command line https://revbayes.github.io/download

  3. Check that revbayes is well installed in your computer by going through this super short tutorial

  4. Install Tracer software to check our MCMC output

  5. Have R with ggplot and ggtree installed for visualizations

Binary state speciation and extinction model (BiSSE)

Carrie Tribble’s lecture slides pdf

BiSSE is a stochastic process that is the composition of two different birth-death stochastic processes connected by a transition rate. The key assumption of a BiSSE model is that the trait can be categorize in two states, each state with its own birth rate \(\lambda\) and death rate \(\mu\) representing the splitting of a lineage or the extinction of a lineage respectively. This is a big assumption because the implication is that the accumulation (or the lack of) of lineages is link to the value of the state (0 or 1) but nothing else.

Often in the literature, including the original BiSSE article, the model is represented graphically by circles and arrows connected as the figure shown below.

Figure 1. BiSSE graphical representation in most published papers. Trait is assumed be be binary, parameters \((\lambda_0, \lambda_1)\) are speciation rates link to each of the states, and parameters \((\mu_0,\mu_1)\) are extinction rates. The transition rates \((q_{01},q_{10})\) indicate how often the value of the trait changes.

The reason why this model is often represented as “circles and arrows” is because it is much easier to communicate than the mathematical representation.

BiSSE using RevBayes

Another way to think about SSE models that is not only the circle and arrow diagrams, or the stochastic differential equations themselves is the graphical model representation. The goal of this introductory workshop is to get you thinking about graphical representations because you can create custom and more complex models without having to build complex equations every time.

We will discuss some of the caveats as well at the end, but one very important key feature to clarify here is that the graphical model is not only a visual representation, but an alternative to writing the math from the model and the inference (Bayesian) simultaneously.

Rev Language

Just a brief reminder that we will be using Rev language and every assignation we use has a meaning in the graphical model world. For more details please refer to (Hoehna et al. 2013 ) 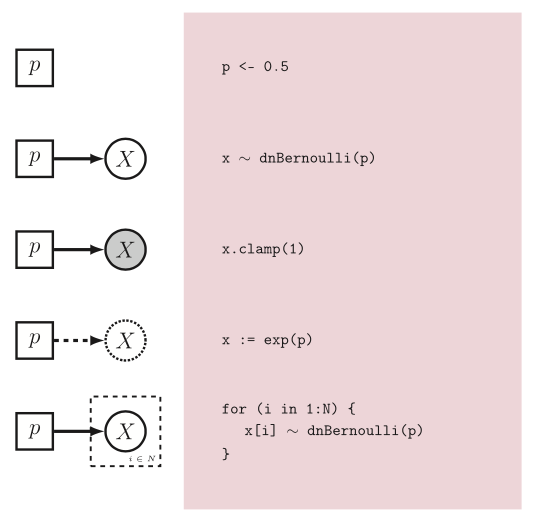Figure 2. From Hoehna et al. 2016. Rev language and its graphical model representation

Trait data utilized for the workshop Polimoneaceae data from Landis, J. et al. 2018. This is a phylogenetic tree of Phlox with selfing and outcrossing data as breeding system binary trait. We will use this dataset as an example of binary trait that could be interesting for diversification.

Trait data .csv, and phylogenetic .tre

RevBayes code

setOption("useScaling","true")
NUM_STATES = 2
### Read in the data
observed_phylogeny <- readTrees("basicdata/poleult.tre")[1]
data <- readCharacterDataDelimited("basicdata/pole_datadis.csv",
stateLabels=2,
type="NaturalNumbers",
delimiter=",",
headers=TRUE)

# Get some useful variables from the data. For example taxa names in the phylogeny
taxa <- observed_phylogeny.taxa()
### Create the fix parameter for the age of the root set to the observed age
root_age <- observed_phylogeny.rootAge()

Indices

# Setting up indices
mvi = 0
mni = 0

Speciation and extinction rates

## Create the constant prior parameters of the diversification rates
## Number of surviving lineages is 165

mx=(ln(165/2)/observed_phylogeny.rootAge())
sx= 0.01
rate_mean <- exp(mx+sx^2)
rate_sd <- exp(2*mx+sx^2)*exp(sx^2-1)

for (i in 1:NUM_STATES) {

### Create a lognormal distributed variable for the diversification rate
log_speciation[i] ~ dnNormal(mean=rate_mean,sd=rate_sd)
log_speciation[i].setValue( rate_mean )
speciation[i] := exp( log_speciation[i] )
moves[++mvi] = mvSlide(log_speciation[i],delta=0.20,tune=true,weight=3.0)

### Create a lognormal distributed variable for the turnover rate
log_extinction[i] ~ dnNormal(mean=rate_mean,sd=rate_sd)
log_extinction[i].setValue( rate_mean )
extinction[i] := exp( log_extinction[i] )
moves[++mvi] = mvSlide(log_extinction[i],delta=0.20,tune=true,weight=3)

}

In graphical modeling what we are doing is connecting fixed with stochastic nodes that have a log-Normal distribution.

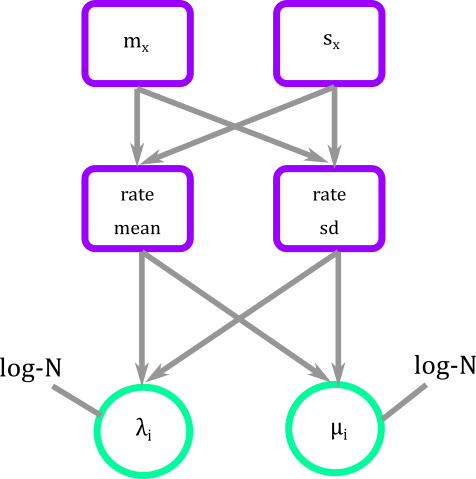
Figure 3. Graphical modeling of diversification rates of BiSSE. Squares represent deterministic nodes, circles represent stochastic nodes

Transition rates

#########################################################
# Set up the transition rate matrix for observed states #
#########################################################
## I defined very loosely my gamma priors for transition rates
shape_pr := 0.5
rate_pr := 1
############### Alternative definition or rate parameter
# Each transition rate between observed states are drawn
# from an exponential distribution with a mean of 10
# character state transitions over the tree.
# rate_pr := observed_phylogeny.treeLength() / 10

q_01 ~ dnGamma(shape=shape_pr, rate=rate_pr)
q_10 ~ dnGamma(shape=shape_pr, rate=rate_pr)

moves[++mvi] = mvScale( q_01, weight=2 )
moves[++mvi] = mvScale( q_10, weight=2 )

######################################################################
# Create the rate matrix for the combined observed and hidden states #
######################################################################
rate_matrix := fnFreeBinary( [q_01, q_10 ], rescaled=false)

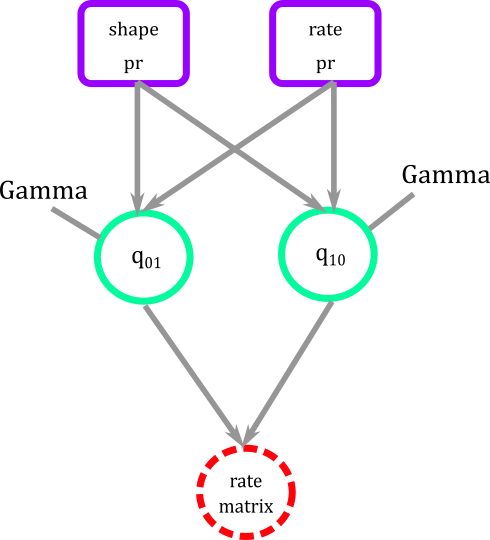
Figure 4. Graphical modeling of transition rates for BiSSE. Squares represent deterministic nodes, circles represent stochastic nodes

What are the moves? There are many many moves available in RevBayes, some specific for certain types of inferences and some others very general.

Treatment of the root

Prior distribution for the root that is Dirichlet because it has two important properties: 1) the values of the vector are between (0,1), and (2) the entries of the vector add to 1.

### Create a constant variable with the prior probabilities of each rate category at the root.
rate_category_prior ~ dnDirichlet( rep(1,NUM_STATES) )
moves[++mvi] = mvDirichletSimplex(rate_category_prior,tune=true,weight=2)

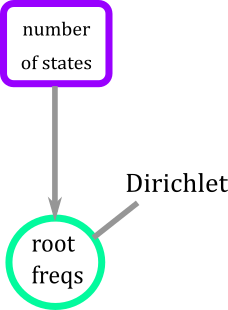
Figure 5. Graphical modeling of the root for BiSSE model. Root has a Dirichlet distribution that is a function of the number of states of the trait.

Sampling bias

### Rho is the probability of sampling species at the present
### fix this to 165/450
sampling <- observed_phylogeny.ntips()/450

Figure 6. Graphical modeling of the sampling bias for BiSSE model. This is simply a fixed node measuring the percentage of lineages not sampled.

Full graphical BiSSE model

As of now you have a series of fixed, stochastic, and deterministic nodes free floating as small pieces of construction blocks.

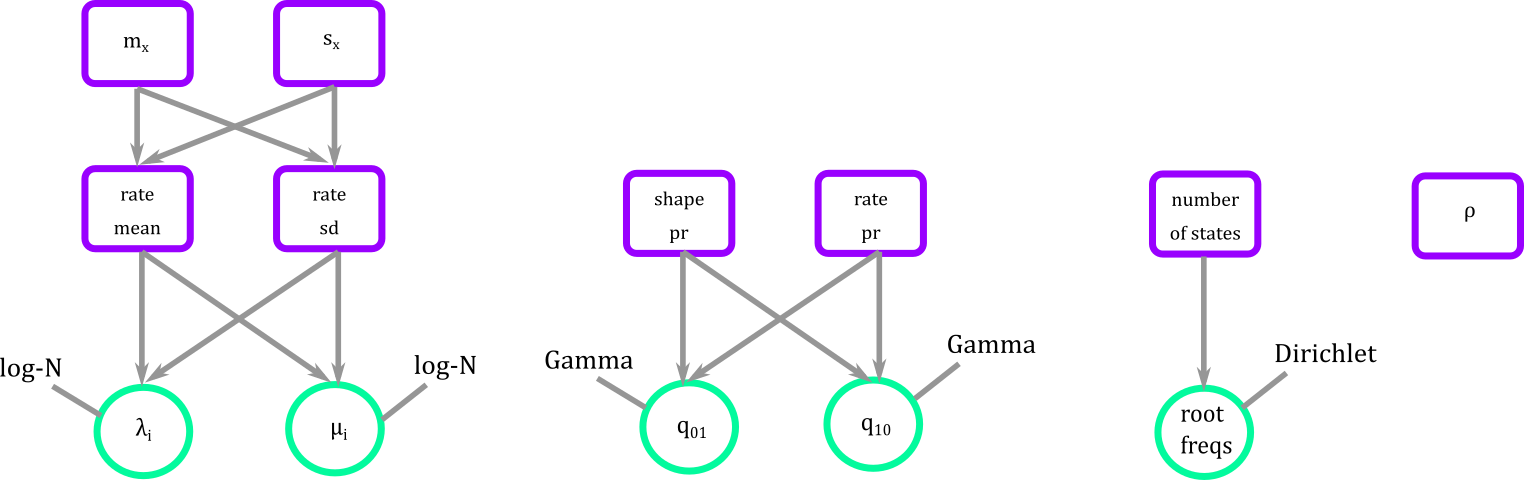Figure 7. Blocks defining the parameters that we will need for the BiSSE.

The connector is a phylogenetic distribution function dnCDBDP the character dependent birth and death process. It is in this function that we plug diversification rates, transition rates, root frequencies, and sampling to create the full BiSSE or any SSE model.

####################################################################
# Building the BiSSE Model as discrete character model+ BD process#
###################################################################

### Here is where I tie speciation, extinction, and Q using a Birth-Death with categories
bissemodel ~ dnCDBDP( rootAge= root_age,
speciationRates   = speciation,
extinctionRates   = extinction,
Q                 = rate_matrix,
pi                = rate_category_prior,
rho               = sampling )

In graphical representation the BiSSE model then looks like Figure 8.

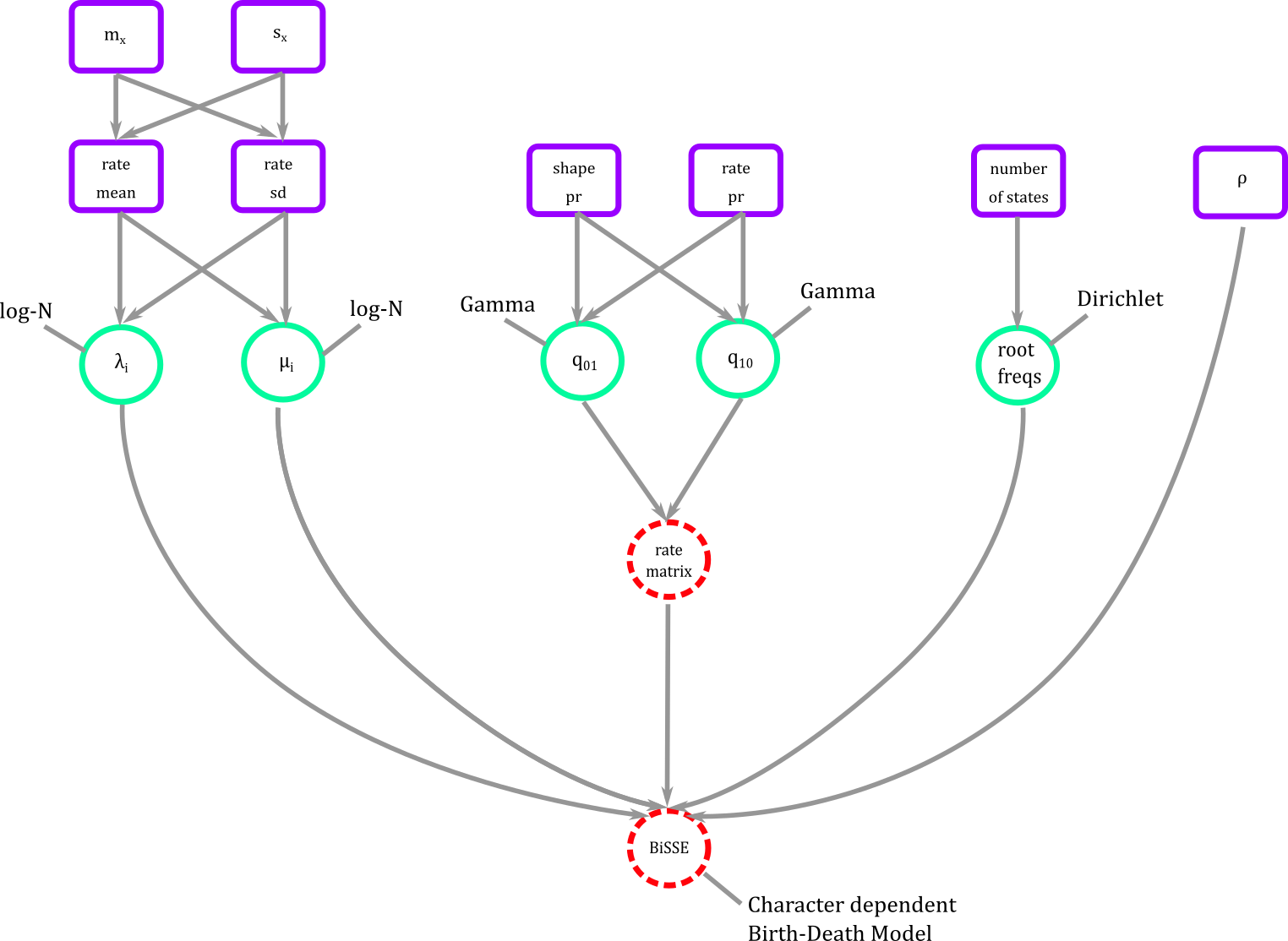Figure 8. BiSSE in graphical modeling. We connect all our modeling blocks using a phylogenetic probability distribution where diversification, transition rates, and root frequencies can be estimated.

Performing statistical inference in RevBayes

Clamping the data

### clamp the model with the "observed" tree and states
bissemodel.clamp( observed_phylogeny )
bissemodel.clampCharData( data )

In graphical model then we have added two more fixed nodes

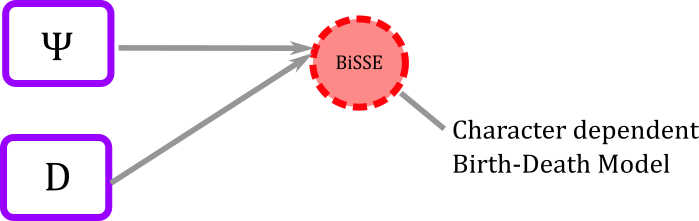
Figure 9. Clamping observed data. In the graphical model world the deterministic node of the model gets some shading to indicate that data has been clamped.

Getting what you want from the MCMC and checking the performance

#############
# The Model #
#############


### workspace model wrapper ###
mymodel = model(rate_matrix)

### set up the monitors that will output parameter values to file and screen
monitors[++mni] = mnFile(filename="output/BiSSE_pole.trees", printgen=1, bissemodel)
monitors[++mni] = mnModel(filename="output/BiSSE_pole.log", printgen=1)
##This monitor was the one giving me trouble type has to be the same that data, however I'm not hundred percent sure whether tree should be the stochastic tree assigned by the clamp or the observed_phylogeny. Will and Sebastian have different inputs

monitors[++mni] = mnJointConditionalAncestralState(tree=observed_phylogeny, cdbdp=bissemodel, type="NaturalNumbers", printgen=1, withTips=true, withStartStates=false, filename="output/anc_states_BiSSE_pole.log")
monitors[++mni] = mnScreen(printgen=10, q_01, q_10, speciation, extinction)

Running the MCMC

################
# The Analysis #
################

### workspace mcmc
mymcmc = mcmc(mymodel, monitors, moves, nruns=1, moveschedule="random")

### pre-burnin to tune the proposals 20% of the sample
mymcmc.burnin(generations=200,tuningInterval=50)

### run the MCMC
mymcmc.run(generations=1000)

Full RevBayes code for BiSSE bisse.Rev

Results visualization

All the results (after 4 days) Opening log-file in tracer

Hidden state speciation and extinction model (HiSSE) and the character independent model

Daniel Caetano’s lecture

Now we are going to fit the HiSSE model

Figure 10. HiSSE model representation in most published papers. Trait is assumed be be binary but it is expanded to four states to accomodate hidden trait affecting diversification. Parameters \((\lambda_{0_A}, \lambda_{1_A},\lambda_{0_B}, \lambda_{1_B})\) are speciation rates link to each of the states, and parameters \((\mu_{0_A},\mu_{1_A},\mu_{0_B},\mu_{1_B})\) are extinction rates. The transition rates \((q_{01},q_{10})\) indicate how often the value of the trait changes, and they could differ within states A and B. The transition rates between hidden states are \((\alpha,\beta)\).

and the character independent model (CID)

Figure 11. CID model representation in most published papers. Trait is assumed be be binary but it is expanded to four states to accomodate hidden trait affecting diversification. We assume here that the trait does not have an effect on diversification and it is only the hidden state that can change speciation and extinction. Parameters \((\lambda_{A},\lambda_{B})\) are speciation rates link to each of the states, and parameters \((\mu_{A},\mu_{B})\) are extinction rates. The transition rates \((q_{01},q_{10})\) indicate how often the value of the trait changes, and they could differ within states A and B. The transition rates between hidden states are \((\alpha,\beta)\).

Practice Find a teammate! Just like we did with the BiSSE model, please try to parse out the code to figure out the graphical model that RevBayes is constructing for HiSSE and CID. We will come back together as a group to discuss similarities and differences and discuss the results of each.

Results

Key References

  • HiSSE and CID: Beaulieu, J.M. and O’Meara, B.C., 2016. Detecting hidden diversification shifts in models of trait-dependent speciation and extinction. Systematic biology, 65(4), pp.583-601.link

  • GeoHiSSE: Caetano, D.S., O’Meara, B.C. and Beaulieu, J.M., 2018. Hidden state models improve state‐dependent diversification approaches, including biogeographical models. Evolution, 72(11), pp.2308-2324.link

  • RevBayes: Höhna, S., Landis, M.J., Heath, T.A., Boussau, B., Lartillot, N., Moore, B.R., Huelsenbeck, J.P. and Ronquist, F., 2016. RevBayes: Bayesian phylogenetic inference using graphical models and an interactive model-specification language. Systematic biology, 65(4), pp.726-736.link

  • BiSSE: Maddison WP, Midford PE, Otto SP. Estimating a binary character’s effect on speciation and extinction. Systematic biology. 2007 Oct 1;56(5):701-10.link

  • BiSSE lack of heterogeneity: Rabosky, D.L. and Goldberg, E.E., 2015. Model inadequacy and mistaken inferences of trait-dependent speciation. Systematic biology, 64(2), pp.340-355.link

  • MuHisse and model selection: Zenil‐Ferguson, R., Burleigh, J.G., Freyman, W.A., Igić, B., Mayrose, I. and Goldberg, E.E., 2019. Interaction among ploidy, breeding system and lineage diversification. New Phytologist. pdf supp1 supp 2 repository

Updated: